Answer:
77.47°
75.96°
26.57°
Explanation:
Given vertices of the triangle:
- A = (−2, 4)
- B = (−3, 8)
- C = (6, 8)
Find the vectors from A to B, B to C and A to C:
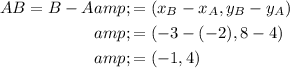
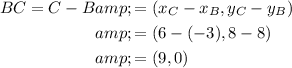
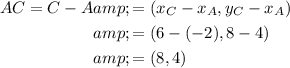
Use Pythagoras Theorem to calculate the magnitudes of the vectors:
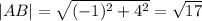
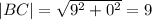
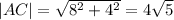

Rearrange the dot product formula to make θ the subject:
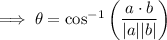
Use the rearranged dot product formula to find the angles between two pairs of vectors.

Angle A
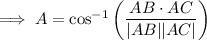
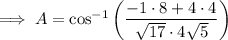
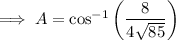
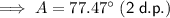
Angle C
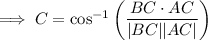
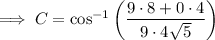
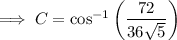
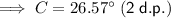
Interior angles of a triangle sum to 180°.
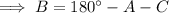

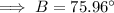
Therefore, the interior angles of the triangle with the given vertices are: