Answer:
9 units²
Explanation:
**Refer to the attached diagram**
The angles in the right triangle FAD (and HBE) are 30-60-90 which means that its sides will be in the ratio 1 : √3 : 2
Let x = the smallest side
Therefore, the sides of the right triangle FAD are in the ratio x : √3x : 2x
This means that:
- the side length of the square = √3x
- the side length of the triangle = x + √3x + x = (2 + √3)x
We are told that the side length of the triangle is 3 + 2√3, so:
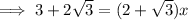


As the side length of the square is √3x, and x = √3,
⇒ side length of the square = √3 x √3 = 3
Now we know the side length of the square, we can calculate the area:
⇒ area of a square = side length x side length = 3 x 3 = 9 units²