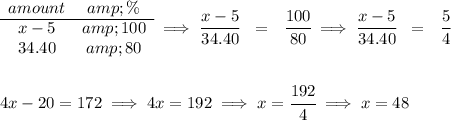the original price was "x", which oddly enough is the 100%.
now, let's pluck out of "x" 5 bucks, so that makes it "x-5", that's our new adjusted 100%, from which the lady at the counter is happy to apply a 20% discount. Now, if the lady discounts 20% off of that "x-5" amount, what Priya is really paying for the sleeping bag is just 100% - 20% = 80%, and we happen to know that that 80% was really $34.40.
now, if "x - 5" is the 100%, and we know that 34.40 is the 80%, what the heck is "x"?