The correct answer is: [D]: "
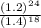 "
"
Explanation:
Given: ( 1.4³ / 1.2⁴)⁻⁶ ;
Note the following properties of exponents:
1)
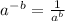 ; {
; {
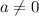 } ; and:
} ; and:
2) the 'power of a fraction' rule:
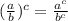 ;
;
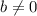 '
'
As such:
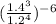 ;
;
= 1 ÷ (
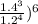 ;
;
=
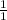 ÷ (
÷ (
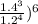 ;;
;;
=
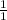 ÷
÷
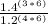 ;
;
Note the follow property of exponents:
"
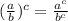 " ; {" b ≠ 0 "}.
" ; {" b ≠ 0 "}.
⇒ =
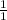 ÷
÷
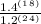
Note: Dividing by a fraction or a number; is the same as multiplying by the reciprocal (invert) of that number.
=
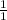 *
*
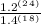 ;
;
= "
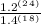 " ;
" ;
which corresponds to:
Answer choice: [D]: "
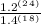 " .
" .
____________
Hope this is helpful! Best of luck!
____________