Answer:
k = 9
length of chord = 2/3
Explanation:
Equation of parabola:
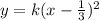
Part 1
If the curve passes through point
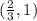 , this means that when
, this means that when
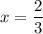 ,
,
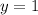
Substitute these values into the equation and solve for
 :
:
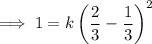

Apply the exponent rule
 :
:
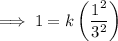
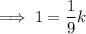
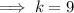
Part 2
- The chord of a parabola is a line segment whose endpoints are points on the parabola.
We are told that one end of the chord is at
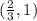 and that the chord is horizontal. Therefore, the y-coordinate of the other end of the chord will also be 1. Substitute y = 1 into the equation for the parabola and solve for x:
and that the chord is horizontal. Therefore, the y-coordinate of the other end of the chord will also be 1. Substitute y = 1 into the equation for the parabola and solve for x:
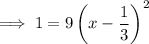
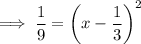
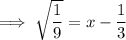
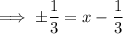
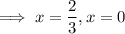
Therefore, the endpoints of the horizontal chord are: (0, 1) and (2/3, 1)
To calculate the length of the chord, find the difference between the x-coordinates:
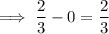
**Please see attached diagram for drawn graph. Chord is in red**