Question

Rosa is making a poster that has a rainbow as part of the design. Using a compass she draws a semicircle with a radius of 18 cm. She draws another semicircle that has a radius of 12 cm as shown. What is the area of the shaded part of the rainbow?

Answer 1

282.7 cm²

Explanation:

Hello There!

To find the area of the shaded area we are going to want to find the area of the whole semi circle and subtract it by the area of the smaller semi circle

To find the area of a semicircle we use this formula

`A=(\pi r^2)/(2)`

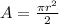
where r = radius

For the large semi circle

The radius of the larger semi circle is 18 cm so we plug in 18 into r in the formula

So..

`A=(\pi 18^2)/(2) \\18^2=324\\324\pi =1017.87602\\(1017.87602)/(2) =508.9380099`

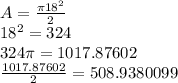
So the area of the whole semi circle is 508.9380099 cm²

Now to find the area of the smaller semi circle

The radius for the smaller semi circle is 12 cm so we plug in 12 into r in the formula

`A=(12^2\pi )/(2) \\12^2=144\\144\pi =452.3893421\\(452.3893421)/(2) =226.1946711`

so the area of the smaller semi circle is 226.1946711cm²

Finally we want to subtract the area of the smaller semi circle from the area of the whole semi circle

508.9380099 - 226.1946711 = 282.7433388

Finally we want to round to the nearest tenth and we get that the area of the rainbow is 282.7 cm²