Answer:
Explanation:
You want the solutions to the rational equation ...
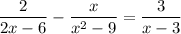
Rewrite
We choose to rewrite the equation in the form f(x) = 0. We can start by subtracting the term on the right side (from both sides).

Solution
The "not-possible values" will be values of x that make the denominator zero: x = ±3. The solution is ...
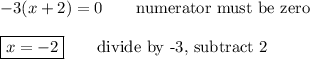
Check
In the original equation, we have ...

__
Additional comment
We like to write the equation as a single fraction compared to zero so that any common factors can be cancelled from numerator and denominator. This helps prevent extraneous solutions. Here, there are none.