Answer:
Jacks Rate: 3 miles per hour
Jills Rate: 4.5 miles per hour
Time: 40 minutes or 2/3 of an hour
Explanation:
Setting up the Algebraic Expressions:
This problem in it self isn't necessarily too complex, but a crucial part of it is taking the context given and somehow making that into a algebraic expression which we can then use to solve the equation.
Assigning Unknowns and Variables:
So let's first assign two unknowns to the rates at which Jack and Jill walk. Since both of there names start with J, I'll use a subscript to differentiate between the two.
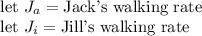
Notice that both have a J, but there is a little letter to the right and below, which is a subscript. This way we can easily tell which person we are referring to while not having to write out their entire name as a variable.
Now let's assign two variables. First let's assign distance:
and let's also assign time to a variable:
Deriving Equations:
Now let's start making some equations! If jack is two miles away from the top of the hill, in general, the distance from the hill can be calculated using the following equation:
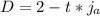
Essentially, Jack starts off with a distance of two miles away, and after one hour, Jack will walk
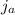miles, this is his rate, what Jake travels in one hour. After another hour passes, he will do the same thing, but twice. So this is why we're multiplying by time. Since for each hour that passes, he will walk a further:
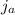miles, meaning he will be that much closer, so we subtract it from 2, the initial distance.
The same logic can be applied to Jill, except with an initial distance of 3 miles and using the unknown:
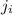which is Jill's rate. So we get the following equation:
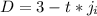
If we're looking for when they reach the top of the hill, that means that the distance from the hill is zero. So let's set both equations to zero.
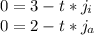
From here let's solve for time for both equations. So let's start with the first equation.
From here let's subtract 3 from both sides to get rid of the 3 on the right side.
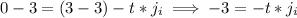
from here let's divide both sides by Jill's rate.
From here let's divide both sides by -1 to get t isolated.
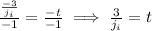
We can essentially apply the same steps to the equation we derived from Jack's rate.
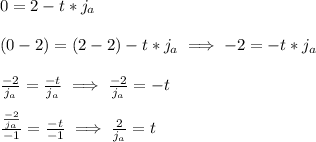
Now we have the equations:
and this represents the time needed to reach the top of the hill (since we set both equations equal to zero)
Substituting and Solving:
From here we need to look once more at the question, specifically where it says: "It takes them the same amount of time to get there". So we set the equations equal to each other.
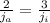
Now we use our last piece of needed context: "Jill walks 1.5 miles per hour faster than Jack". We can set up one more equation:
.
This is super useful to have, since we can now make a substitution give this equation, converting our two-variable equation into a one-variable equation, allowing us to solve for one numerical value.
We have:
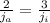and we know that:
, so let's simply plug in
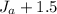for
.
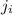This gives us the equation:
.
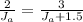Cross Multiply:
.
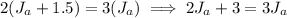Subtract
:
.
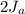We can solve for Jills value, since Jill's value is just 1.5 miles per hour more than this, so
Now let's take Jacks value and substitute it into his time equation
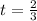
we can keep this in hours, or we can convert this into minutes. We can convert this in to minutes by multiplying the amount of minutes in an hour by 2/3, so:
