Answer:
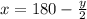
Explanation:
Our goal here is to isolate
 on one side of the equals sign
on one side of the equals sign
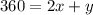
Here we have 2 terms on the right side of the equals sign,
 and
and

in order isolate the
 term we must subtract
term we must subtract

However, if we subtract
 from one side of the equation we must also do the same to the other side to a maintain balanced equation.
from one side of the equation we must also do the same to the other side to a maintain balanced equation.
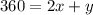
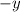
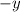
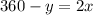
Now to remove "2" from
 we must do the opposite of multiplication, which is division.
we must do the opposite of multiplication, which is division.
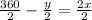
simplify.
