Answer:
H (13, -16)
Explanation:
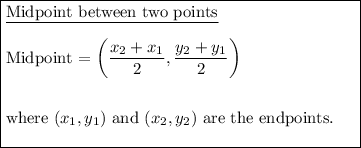
Given:
- Endpoint (x₁, y₁) = G (-7, 24)
- Endpoint (x₂, y₂) = H
- Midpoint = M (3, 4)
Substitute the given endpoint G and midpoint M into the midpoint formula:
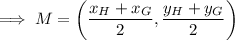
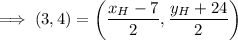
x-value of endpoint H:
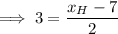

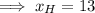
y-value of endpoint H:
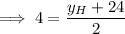
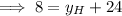
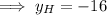
Therefore, the coordinates of endpoint H are: