Question

A person places $6520 in an investment account earning an annual rate of 2.5%,

compounded continuously. Using the formula V = Pert, where V is the value of the
account in t years, P is the principal initially invested, e is the base of a nfitural
logarithm, and r is the rate of interest, determine the amount of money, to the nearest
cent, in the account after 3 years.

Answer 1

Given:

Principal value = $6520

Annual rate of interest = 2.5% compounded continuously.

Time = 3 years

To find:

The amount of money after three years.

Solution:

Formula for the value of the amount is:

`V=Pe^(rt)`

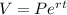
Where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest.

Putting
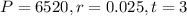`P=6520,r=0.025,t=3`, we get

`V=6520e^((0.025)(3))`

`V=6520e^(0.075)`

`V=7027.80466`

`V\approx 7027.80`

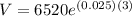
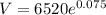
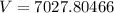
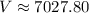
Therefore, the amount of money after three years is about $7027.80.