Given:
Principal value = $6520
Annual rate of interest = 2.5% compounded continuously.
Time = 3 years
To find:
The amount of money after three years.
Solution:
Formula for the value of the amount is:
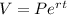
Where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest.
Putting
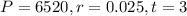 , we get
, we get
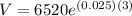
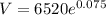
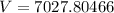
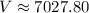
Therefore, the amount of money after three years is about $7027.80.