Question

Describe the end behavior of the function -2x^3-13x^2+8x+52

Answer 1

`\text{as x} \to \infty, \ \text{y} \to -\infty\\\\\text{as x} \to -\infty, \ \text{y} \to \infty`

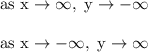
Rises to the left; falls to the right

============================================================

Step-by-step explanation:

The leading term is what determines the end behavior of any polynomial function.

• Given polynomial: -2x^3-13x^2+8x+52
• Leading term: -2x^3

The leading term has the largest exponent. The other terms will have no effect on the end behavior.

As x gets really large in the positive direction, so does x^3. But the -2 out front will flip to have y go to negative infinity.

Therefore:
`\text{as x} \to \infty, \ \text{y} \to -\infty`

We can informally think of this as "falls to the right".

---------------------------

As x heads to the left, x^3 becomes further negative. But -2 out front makes -2x^3 to be positive.

So
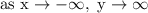`\text{as x} \to -\infty, \ \text{y} \to \infty` aka "rises to the left".

Whatever x does, y does the opposite. If x goes positive, then y goes negative and vice versa.

-------------------------

The end behavior is therefore

`\text{as x} \to \infty, \ \text{y} \to -\infty\\\\\text{as x} \to -\infty, \ \text{y} \to \infty`

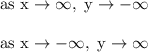
x and y are opposite.

We can summarize that notation as saying "rises to the left, falls to the right".

See the graph below. I used GeoGebra to make the graph, but you can use Desmos or any other tool you prefer.