Answer:
Explanation:
We have been given that -- The length of a rectangular parking lot is 16 yards greater than 3 times its width, x, in yards
Length of parking lot is 16 + 3x
Width of parking lot is x
We have to write the function f(x) that describes the area, in square yards, as a function of the width, x
Area of rectangle is Length × width
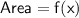
put value of length and width here,
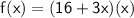
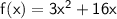
Therefore, f(x) = 3x² + 16x