Answer:
Slope: 3/2
y-intercept: 9
Explanation:
Slope-Intercept Form:
Slope-Intercept Form is given in the form:
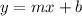 , where
, where
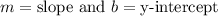 .
.
So it's very convenient to have a linear equation in this form to identify the slope and y-intercept. To get into this form, we simply need to isolate the y-value.
Converting to Slope-Intercept Form:
We start with the initial equation:

The first step to isolating "y" is to move any terms on the same side as the "y" variable to the other side. So let's move the 3x term to the other side, by adding 3x to both sides.
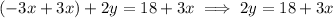
From here, the only thing that is with the "y" variable is the coefficient. The
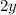 is the same thing as:
is the same thing as:
 . We want to get rid of the 2, which we do by dividing by 2, to cancel out the multiplication by 2.
. We want to get rid of the 2, which we do by dividing by 2, to cancel out the multiplication by 2.
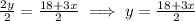
Now from here we want to distribute the division by 2 as such:
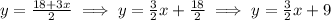
So now we have the equation:

this is in the slope-intercept form:

in this form the coefficient of x is the slope, so 3/2 is the slope. The constant is the y-intercept, so 9 is the y-intercept.