Question

Express f(x) in the form f(x) = (x - k)q(x)+r for the given value of k.

f(x)= x^3+ 4x² + 5x + 2, k= -2

Answer 1

Given:

`f(x)=x^3+4x^2+5x+2,k=-2`

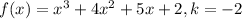
To find:

The the given function in the form
`f(x)=(x-k)q(x)+r`.

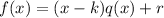Solution:

We have,

`f(x)=x^3+4x^2+5x+2`

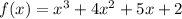
The coefficients of f(x) are 1, 4, 5, 2.

Divide the given function by (x+2) by using synthetic division as shown below:

-2 | 1 4 5 2

-2 -4 -2

_____________________

1 2 1 0

_____________________

Bottom row represent the quotient and last element of the bottom row is the remainder.

Degree of the function is 3 and the degree of division is 1. So, the degree of the quotient is 3-1 = 2.

So, the quotient is
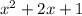`x^2+2x+1` and the remainder is 0.

Now,

`f(x)=(x-k)q(x)+r`

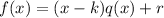
Here, q(x) is the quotient and r is the remainder.

`f(x)=(x-k)(x^2+2x+1)+0`

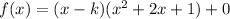
Therefore, the required answer is
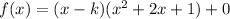`f(x)=(x-k)(x^2+2x+1)+0`.