Given:

To find:
The the given function in the form
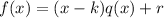 .
.
Solution:
We have,
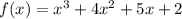
The coefficients of f(x) are 1, 4, 5, 2.
Divide the given function by (x+2) by using synthetic division as shown below:
-2 | 1 4 5 2
-2 -4 -2
_____________________
1 2 1 0
_____________________
Bottom row represent the quotient and last element of the bottom row is the remainder.
Degree of the function is 3 and the degree of division is 1. So, the degree of the quotient is 3-1 = 2.
So, the quotient is
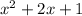 and the remainder is 0.
and the remainder is 0.
Now,
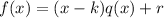
Here, q(x) is the quotient and r is the remainder.

Therefore, the required answer is
 .
.