Given:
The areas of two similar squares are 16m² and 49m².
To find:
The scale factor of their side lengths.
Solution:
We know that the ratio of the areas of the similar squares is proportional to the ratio of square of there sides.
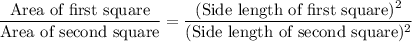
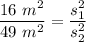
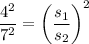
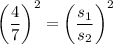
Taking square root on both sides, we get

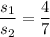
Now, the scale factor is the ratio of side length of second square to the side length of first square.
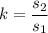
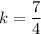
Therefore, the scale factor of their side lengths is
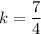 .
.