Answer:
See below.
Step-by-step explanation:
Here using F = ma , we need to derive the fire and second equation of motion.
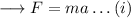
As we know that the rate of change of velocity is called acceleration. Therefore,
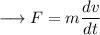
From equation (i) we have,
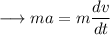
If the mass is constant,
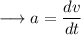
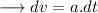
On integrating both sides,
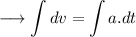
LHS will be integrated from v₀ to v and RHS will be integrated from 0 to t , as ;
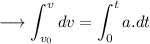
Here a is constant , so ;
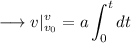
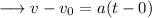
Adding v₀ both sides,
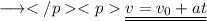
Hence we have derived the First equation of motion.
For second , as we know that ,
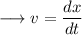
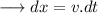
Integrating both sides, we have;
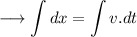
Putting the limits,
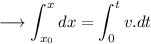
From first equation,
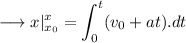
Distribute ,
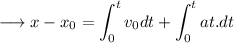
![\displaystyle \longrightarrow x-x_0= v_0(t-0)+a\bigg[(t^2)/(2)\bigg]^t_0\\](https://img.qammunity.org/2023/formulas/physics/college/fb88wquxrds6lan993gpsn2607cm397xam.png)
Simplify,
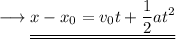
Therefore we have derived the second equation of motion.
And we are done!