Answer:
a) x = -2
b) 8 integer values
Explanation:
Matthew's solution is correct as far as it goes. However, he failed to take into account the possibility of negative square roots.
His solution might rightly look like ...
3 < 3x² ≤ 75
1 < x² ≤ 25 . . . . . divide by 3
1 < ±x ≤ 5 . . . . . . take the square root
Separating the results:
1 < x ≤ 5
-1 > x ≥ -5 . . . . . . multiply by -1
a)
The value x=-2 shows Matthew's solution is incorrect:
3 < 3(-2)² ≤ 25 ⇒ 3 < 12 ≤ 25 . . . true
__
b)
x can have the integer values {-5, -4, -3, -2, 2, 3, 4, 5}, a total of 8 values.
__
In the attached, the white space (and dashed line) are the solution set. The shaded areas (and solid line) are excluded from the solution set.
_____
Additional comment
It can be helpful to remember that ...
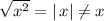
That is, values of x may be negative, but the positive square root will only show you a positive value.