Answer:
x = 2.5 mm
Explanation:
A compound shape is made up of two or more basic shapes.
From inspection of the given compound shape, we can see that it is made up of two rectangles.

Dimensions of the smaller rectangle:
Dimensions of the larger rectangle:
Therefore, the equation for the area of the compound shape is:
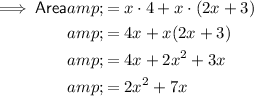
Given the area of the compound shape is 30 mm², substitute this value into the found equation for area and solve for x:

As length is positive, x = 2.5 mm only.