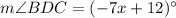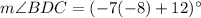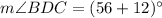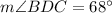Question

I need help with this 2. Please help.

Answer 1

`m\angle BDC = 68\textdegree`

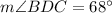
Explanation:

Using the given information, we can deduce that angles BDC and ADC are supplementary; their measures add to 180°.

This can be represented by the following equation:

`(-7x + 12)\textdegree + (-8x+48)\textdegree = 180\textdegree`

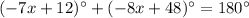
First, solve for x.

`-15x\textdegree + (12 + 48)\textdegree = 180\textdegree`

`-15x \textdegree = (180 - 60) \textdegree`

`-15x\textdegree = 120\textdegree`

`x\textdegree = -8\textdegree`

`x = -8`

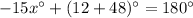
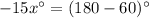
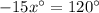
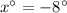
Then, substitute x into the expression for BDC.

`m\angle BDC = (-7x+12)\textdegree`

`m\angle BDC = (-7(-8) + 12)\textdegree`

`m\angle BDC = (56 + 12)\textdegree`

`m\angle BDC = 68\textdegree`