Answer:
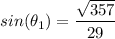
Explanation:
The parameters of the angle θ₁ are;
The location of θ₁ = Quadrant II
cos(θ₁) = -22/29
We note the following;
1) The sine of an angle in quadrant II is positive
2) The cosine of an angle in quadrant II is negative,
2) The cos of an angle = The adjacent leg length to the reference angle divided by the hypotenuse length of a right triangle
3) With regards to the right triangle for finding cos(θ₁)
The adjacent leg length = -22 (The x-axis is negative in quadrant II)
The hypotenuse length = 29
The negative sign is obtained from the value of cosine in the quadrant
Therefore, by Pythagoras' theorem, for a right triangle, we have;
The opposite leg length to 'θ₁' = √(29² - 22²) = √(357)
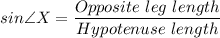
Therefore, we have;
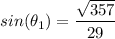 .
.