Question

The inner cylinder of a long, cylindrical capacitor has radius r and linear charge density +λ. It is surrounded by a coaxial cylindrical conducting shell with inner radius r and linear charge density -λ. (a) What is the energy density in the region between the conductors at a distance r from the axis?b) Integrate the energy density calculated in part (a) over the volume between the conductors in a length L of the capacitor to obtain the total electric-field energy per unit length

Answer 1

Hi there!

a)

We can begin by using the equation for energy density.

`U = (1)/(2)\epsilon_0 E^2`

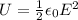
U = Energy (J)

ε₀ = permittivity of free space

E = electric field (V/m)

First, derive the equation for the electric field using Gauss's Law:

`\Phi _E = \oint E \cdot dA = (Q_(encl))/(\epsilon_0)`

Creating a Gaussian surface being the lateral surface area of a cylinder:

`A = 2\pi rL\\\\E \cdot 2\pi rL = (Q_(encl))/(\epsilon_0)\\\\Q = \lambda L\\\\E \cdot 2\pi rL = (\lambda L)/(\epsilon_0)\\\\E = (\lambda )/(2\pi r \epsilon_0)`

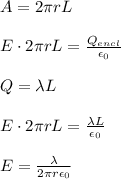
Now, we can calculate the energy density using the equation:

`U = (1)/(2) \epsilon_0 E^2`

Plug in the expression for the electric field and solve.

`U = (1)/(2)\epsilon_0 ((\lambda)/(2\pi r \epsilon_0))^2\\\\U = (\lambda^2)/(8\pi^2r^2\epsilon_0)`

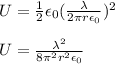
b)

Now, we can integrate over the volume with respect to the radius.

Recall:

`V = \pi r^2L \\\\dV = 2\pi rLdr`

Now, we can take the integral of the above expression. Let:

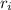`r_i` = inner cylinder radius

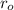`r_o` = outer cylindrical shell inner radius

Total energy-field energy:

`U = \int\limits^(r_o)_(r_i) {U_D} \, dV = \int\limits^(r_o)_(r_i) {2\pi rL *U_D} \, dr`

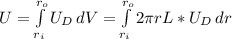
Plug in the equation for the electric field energy density and solve.

`U = \int\limits^(r_o)_(r_i) {2\pi rL *(\lambda^2)/(8\pi^2r^2\epsilon_0)} \, dr\\\\U = \int\limits^(r_o)_(r_i) { L *(\lambda^2)/(4\pi r\epsilon_0)} \, dr\\`

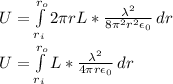
Bring constants in front and integrate. Recall the following integration rule:

`\int {(1)/(x)} \, dx = ln(x) + C`

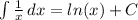
Now, we can solve!

`U = (\lambda^2 L)/(4\pi \epsilon_0)\int\limits^(r_o)_(r_i) { (1)/(r)} \, dr\\\\\\U = (\lambda^2 L)/(4\pi \epsilon_0) ln(r)\left \| {{r_o} \atop {r_i}} \right. \\\\U = (\lambda^2 L)/(4\pi \epsilon_0) (ln(r_o) - ln(r_i))\\\\U = (\lambda^2 L)/(4\pi \epsilon_0) ln((r_o)/(r_i))`

To find the total electric field energy per unit length, we can simply divide by the length, 'L'.

`(U)/(L) = (\lambda^2 L)/(4\pi \epsilon_0) ln((r_o)/(r_i))(1)/(L) \\\\(U)/(L) = \boxed{(\lambda^2 )/(4\pi \epsilon_0) ln((r_o)/(r_i))}`

And here's our equation!