Question

Solve the equation for the interval [0, 2pi). 2sin^2x = sin x

A) 0, pi, pi/6, 5pi/6
B) pi/6, 5pi/6
C) pi/3, 2pi/3
D) pi/2, 3pi/2, pi/3, 2pi/3​

Answer 1

A

Explanation:

We want to solve the equation:

`2\sin^2(x)=\sin(x)`

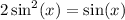
For the interval [0, 2π).

First, we can move all the terms to one side. Start off by subtracting sin(x) from both sides:

`2\sin^2(x)-\sin(x)=0`

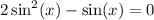
We can factor:

`\sin(x)\left(2\sin(x)-1\right)=0`

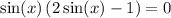
By the Zero Product Property:

`\sin(x)=0\text{ or } 2\sin(x)-1=0`

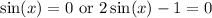
Solve for each case:

`\displaystyle \sin(x)=0\text{ or } \sin(x)=(1)/(2)`

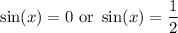
Use the unit circle to solve:

`\displaystyle x=\left\{0, (\pi)/(6),(5\pi)/(6), \pi\right\}`

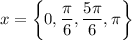
Hence, our answer is A.

*Please note that we should not simply divide both sides by sin(x) to acquire 2sin(x) = 1. The problem with the operation is that we are dividing by sin(x), yet we do not know what the value of x is. Thus, one or more values of x may result in sin(x) = 0, and we cannot divide by 0. Hence, we are required to subtract and then factor, unless the question specifically states that sin(x) ≠ 0.