Simplified Recap:
PQR and XYR are similar.
PQ: 4 inches (shortest side)
PR: 9 inches
QR: 12 inches (longest side)
Solving:
Because they are similar triangles, we know that the sides of one triangle are proportional to the ones on the other. Therefore, the smallest side of PQR is proportional to the smallest side of XYZ. Now, we just need to figure out the constant of proportionality , and we can do that by dividing the smallest side of XYZ triangle by the smallest side of PQR.

Now we know that the constant of proportionality is 4. All we have to do now is solve the problem. The question is asking what the longest side of XYZ is, and to find that we just need to multiply the longest side of PQR by our constant of proportionality.
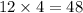
Therefore, our answer is 48.