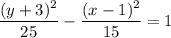Answer:
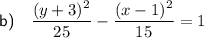
Explanation:

Given:
- center (1, -3)
- vertex (1, 2)
- focus (1, -3+2√10)
As the x-values of the given center, vertex and focus are the same, the hyperbola is vertical (opening up and down).
Given the center is (1, -3):
Use the vertices formula (h, k±a) to find a:
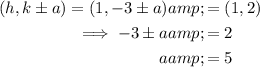
Use the foci formula (h, k±c) to find c:
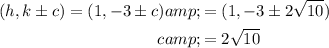
Use the found values of a and c with Pythagoras Theorem to find b²:

Therefore:
- h = 1
- k = -3
- a² = 5² = 25
- b² = 15
Substitute the found values into the hyperbola formula to create an equation of the hyperbola with the given parameters: