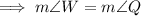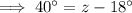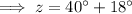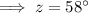Answer:
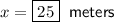
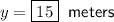
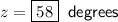
Explanation:
Similar Triangles
- Corresponding sides are always in the same ratio.
- Corresponding angles are the same size.
If ΔWXY ~ ΔQRS then:
- WX : QR = XY : RS = WY : QS
Therefore:
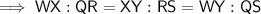
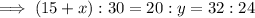
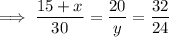
Solving for x:
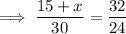
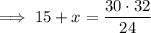
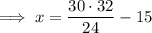
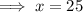
Solving for y:
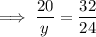
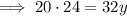
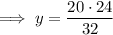
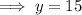
If ΔWXY ~ ΔQRS then:
- m∠W = m∠Q
- m∠X = m∠R
- m∠Y = m∠S
Therefore, solving for z: