Answer:
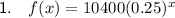
(-1, 41600) and (3, 162.5)
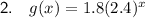
3. Sarah is incorrect.
Explanation:

Question 1
The y-intercept is when x = 0.
Therefore, from inspection of the given table, the y-intercept is 10400:
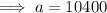
Substitute point (1, 2600) and a = 10400 into the exponential function and solve for b:

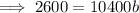
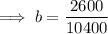
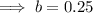
Therefore, the equation of the function is:
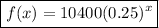
Find the value of x when f(x) = 41600:
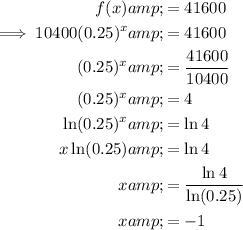
Find the value of f(x) when x = 3:
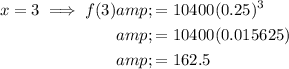
Therefore, the completed table is:

Question 2
Given points:
Substitute the given points into the exponential formula g(x) = abˣ
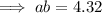
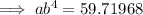
To find b, divide the equations:
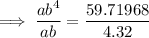
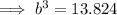
![\implies b=\sqrt[3]{13.824}](https://img.qammunity.org/2023/formulas/mathematics/college/n097gw0hczvkdiq1w3ivsh4i7mbihwidu4.png)
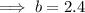
Substitute one of the points and the found value of b into the equation and solve for a:
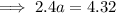
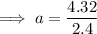
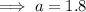
Therefore, the equation of the function is:
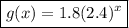
Question 3
Sarah is incorrect. For an exponential function in the form a · bˣ:
- If a > 0 and b > 1 then it is an increasing function.
- If a > 0 and 0 < b < 1 then it is a decreasing function.