Answer:
x = log₂₃(6) = log(6)/log(23)
Explanation:
You want a description of the solution to the exponential equation 23^x = 6.
Logs
The relevant logarithm relations are ...
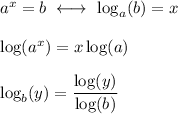
Solution
Angie can use the definition of a logarithm, shown above as the first of the relevant logarithm relations, to rewrite the equation as a log equation:
log₂₃(6) = x
In order to evaluate this expression, Angie can use the change of base formula to write the value of x in terms of logarithms we can find the values of :
x = log₂₃(6) = log(6)/log(23)
This is essentially identical to the solution Angie would reach if she were to take the logarithms of both sides of the original equation, then solve for x.
log(23^x) = log(6) . . . . take logs of both sides
x·log(23) = log(6) . . . . simplify log(23^x)
x = log(6)/log(23) . . . . divide by the coefficient of x
__
Additional comment
We prefer the latter approach, as it gets you directly to something you can evaluate. The change of base formula is only needed if you want to write the solution as a base-23 logarithm.
x ≈ 0.571444
<95141404393>