Answer:
14.2
Explanation:
Hi there!
We are given a 30-60-90 triangle
The triangle is a right triangle, since one of the angles measures 90 degrees
We are also given that the length of the hypotenuse (the side OPPOSITE from the right angle) is 6
We want to find the perimeter of the triangle
There are special formulas to find the other sides of the triangle, if we know that:
a. the triangle is a right triangle
b. we know the length of the hypotenuse
These two formulas are:
- If the length of the hypotenuse in a triangle is a, then the length of the side OPPOSITE from the 30 degree angle is
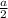
- The length of the side OPPOSITE from the 60 degree angle is

In this problem, we are given that a=6, so that means that in order to find the length of the other sides:
The length of the side opposite from the 30° angle:
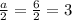
The length of the side opposite from the 60° angle:
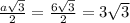 , or about 5.2
, or about 5.2
Now, to find the perimeter, we add the lengths of these sides together.
6 + 3 + 5.2 = 14.2
Hope this helps!