Question

Abbey and Mia are in the basement playing pool. On Abbey's recent shot, the cue ball was moving east at 91 cm/s when it struck the slower 8-ball moving in the same direction at 18 cm/s. The 8-ball immediately speeds up to 62 cm/s. Determine the post-collision velocity of the cue ball. (Assume all balls have the same mass.)

Answer 1

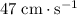`47\; {\rm cm\cdot s^(-1)}` to the east.

Step-by-step explanation:

When an object of mass
`m` travels at a velocity of
`v`, the momentum
`p` of that object will be
`p = m\, v`.

Let
`m` denote the mass of one ball.

Before the collision:

• Momentum of the cue ball:
  `p(\text{cue, before}) = m\, v(\text{cue, before})`.
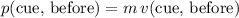• Momentum of the numbered ball:
  `p(\text{number, before}) = m\, v(\text{number, before})`.

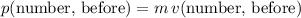Hence, the total momentum before the collision was:

`\begin{aligned} & p(\text{cue, before}) + p(\text{number, before}) \\ &= m\, v(\text{cue, before}) + m\, v(\text{number, before})\end{aligned}`.

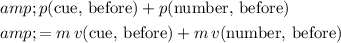Likewise, the total momentum right after the collision would be:

`\begin{aligned} & p(\text{cue, after}) + p(\text{number, after}) \\ &= m\, v(\text{cue,after}) + m\, v(\text{number, after})\end{aligned}`.

Momentum is supposed to be conserved during the collision. In other words, total momentum should be the same immediately before and after the collision. Hence:

`\begin{aligned} & p(\text{cue, before}) + p(\text{number, before}) \\ &= p(\text{cue, after}) + p(\text{number, after})\end{aligned}`.

`\begin{aligned} & m\, v(\text{cue, before}) + m\, v(\text{number, before}) \\ &= m\, v(\text{cue, after}) + m\, v(\text{number, after})\end{aligned}`.

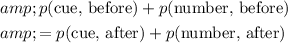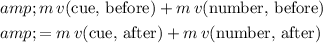Assume that positive velocities denote motion to the east.

In this question,
`v(\text{cue, before})`,
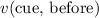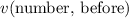`v(\text{number, before})`, and
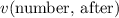`v(\text{number, after})` are all given. Rearrange this equation to find
`v(\text{cue, after})`:

`\begin{aligned}& m \, v(\text{cue, after}) \\ &= m\, v(\text{cue, before}) \\ &\quad\quad + m\, v(\text{number, before}) \\ &\quad\quad - m\, v(\text{number, after}) \end{aligned}`.

`\begin{aligned}& v(\text{cue, after}) \\ &= v(\text{cue, before}) \\ &\quad\quad + v(\text{number, before}) \\ &\quad\quad - v(\text{number, after}) \\ &= 91\; {\rm cm \cdot s^(-1)} + 18\; {\rm cm\cdot s^(-1)} - 62\; {\rm cm\cdot s^(-1)} \\ &= 47\; {\rm m\cdot s^(-1)}\end{aligned}`.

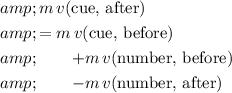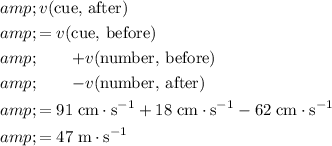Since the result is greater than zero, the direction of motion of the cue ball after the collision will also be to the east.