Answer:
x = 5
Explanation:
Looking at the ratios of height to base:
Smaller triangle 3x + 1 : 12
Larger triangle 4x : 3 + 12 = 4x : 15
Therefore as triangles are similar:
3x + 1 : 12 = 4x : 15
Write as fractions:
⇒
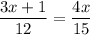
Cross multiply and solve for x:
⇒ 15(3x + 1) = 12 · 4x
⇒ 45x + 15 = 48x
⇒ 15 = 3x
⇒ x = 5