Angle SRT is 72.
Let's consider that RS is the radius of the circle, and ST is a part of the circumference of the circle, given as 6π.
The formula to find the length of an arc of a circle is:
Arc length=
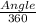 ×2πr, where r is the radius of the circle.
×2πr, where r is the radius of the circle.
Here, the length of the arc ST is given as 6π, and the radius RS is 15. So, we can set up an equation to find the angle subtended by the arc ST at the center of the circle:
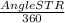 ×2π×15=6π
×2π×15=6π
Let's solve for the angle:
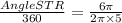
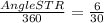
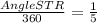
Now, solve for the angle:
Angle SRT=
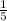 ×360
×360
Angle SRT=72
So, angle SRT is 72