Question

Help please!! This is actually so confusing

Answer 1

Answer:
`(√(55))/(8)`

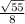
This is the same as writing sqrt(55)/8 where the 8 is not inside the square root.

=====================================================

Step-by-step explanation:

Draw a right triangle in the quadrant Q1, which is in the northeast corner.

We're given
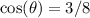`\cos(\theta) = 3/8`. Recall that cosine is the ratio of adjacent over hypotenuse.

`\cos(\text{angle}) = \text{adjacent/hypotenuse}`

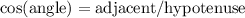
This right triangle will have an adjacent side of 3 and hypotenuse of 8.

Refer to the diagram below.

Use the pythagorean theorem
`a^2+b^2 = c^2` to find the missing side is exactly
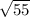`√(55)`, which is the opposite side of angle theta.

Then as one last step, we would say:

`\sin(\text{angle}) = \text{opposite/hypotenuse}\\\\\\\sin(\theta) = (√(55))/(8)`

--------------

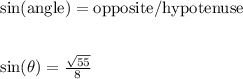
A very similar approach is to use the pythagorean trig identity

`\sin^2(\theta)+\cos^2(\theta) = 1`

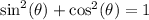
Solving for sine gets us

`\sin(\theta)=√(1-\cos^2(\theta) )`

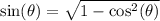
Sine is positive in Q1.

Then plug in
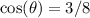`\cos(\theta) = 3/8` and simplify. You should get the answer mentioned above.