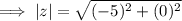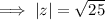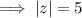Answer:
(-5, 0)
|z| = 5
Explanation:
Complex numbers can be represented on an Argand diagram.
The x-axis is called the real axis and the y-axis is called the imaginary axis.
The complex number z = x + iy is represented on the diagram by the point P(x ,y), where x and y are Cartesian coordinates.
Therefore, the complex number z = -5 can be represented on the Argand diagram by the point:
The absolute value of a complex number is the magnitude of its corresponding vector.
For a complex number z = x + iy, the absolute value is given by:
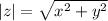
Therefore, the absolute value of complex number z = -5 is: