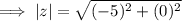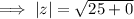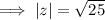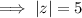Question

Did I solve the absolute value right, when solving I used
`√((5)^2+(0)^2)`

which I only got 5, but I feel like that felt a little too easy and wanted to make sure i answer this question right.

Answer 1

(-5, 0)

|z| = 5

Explanation:

Complex numbers can be represented on an Argand diagram.

The x-axis is called the real axis and the y-axis is called the imaginary axis.

The complex number z = x + iy is represented on the diagram by the point P(x ,y), where x and y are Cartesian coordinates.

Therefore, the complex number z = -5 can be represented on the Argand diagram by the point:

• (-5, 0)

The absolute value of a complex number is the magnitude of its corresponding vector.

For a complex number z = x + iy, the absolute value is given by:

`|z|=√(x^2+y^2)`

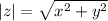
Therefore, the absolute value of complex number z = -5 is:

`\implies |z|=√((-5)^2+(0)^2)`

`\implies |z|=√(25+0)`

`\implies |z|=√(25)`

`\implies |z|=5`