Question

I tried the cosine rule and the sine rule but i dont get why the answer is wrong.

Answer 1

93.2° (nearest tenth)

Explanation:

`\boxed{\begin{minipage}{7.6 cm}\underline{Sine Rule} \\\\\\$(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c) $\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

From inspection of the given triangle:

• B = 38°
• b = 9 cm
• c = 11 cm

Substitute the values into the sine rule to find the measure of angle C:

`\implies (\sin B)/(b)=(\sin C)/(c)`

`\implies (\sin 38^(\circ))/(9)=(\sin C)/(11)`

`\implies \sin C=(11\sin 38^(\circ))/(9)`

`\implies C=\sin ^(-1) \left((11\sin 38^(\circ))/(9)\right)`

`\implies C=48.80523914...^(\circ)`

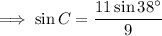
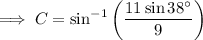
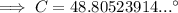
Interior angles of a triangle sum to 180°.

`\implies A+B+C=180^(\circ)`

`\implies A+38^(\circ)+48.80523914...^(\circ)=180^(\circ)`

`\implies A=93.19476086...^(\circ)`

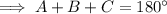
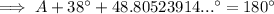
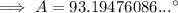
Therefore, the size of angle A is 93.2° (nearest tenth).