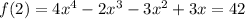Question

Hi can someone solve this with steps?

Answer 1

42

Explanation:

Given function:

`f(x)=4x^4-2x^3-3x^2+3x`

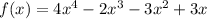
Use the method of synthetic substitution to find the value of the function when x = 2.

Place the value of x in the left box and write the coefficients of the function in descending order, remembering to write a zero for the coefficient of any missing term.

(As there is no constant term in this function, the last coefficient should be written as zero).

`4x^4-2x^3-3x^2+3x`

`\begin{array}c2&4&\:\:-2&\;\;-3&\;\:\:\:\:3&\;\;0\\\cline{1-1} \end{array}`

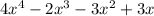
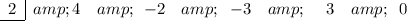
Bring the leading coefficient down:

`\begin{array}ccccc2 &4&-2&-3&3&0\\\cline{1-1}&\downarrow &&&\\\cline{2-6}&4\end{array}`

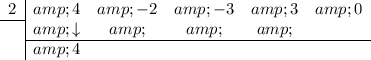
Multiply the number you brought down with the number in the box and put the result in the next column (under the -2):

`\begin{array}rrrrr2 &4&-2&-3&3&0\\\cline{1-1}&\downarrow &8&&\\\cline{2-6}&4\end{array}`

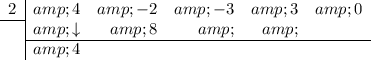
Add the two numbers in the second column together and put the result under them in the bottom row:

`\begin{array}c2 &4&-2&-3&3&0\\\cline{1-1}&\downarrow &8&&\\\cline{2-6}&4&6\end{array}`

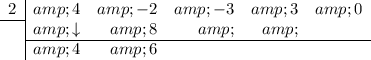
Repeat:

`\begin{array}rrrrr2 &4&-2&-3&3&0\\\cline{1-1}&\downarrow &8&12&\\\cline{2-6}&4&6&9\end{array}`

`\begin{array}rrrrr2 &4&-2&-3&3&0\\\cline{1-1}&\downarrow &8&12&18\\\cline{2-6}&4&6&9&21\end{array}`

`\begin{array}c2 &4&-2&-3&3&0\\\cline{1-1}&\downarrow &8&12&18&42\\\cline{2-6}&4&6&9&21&42\end{array}`

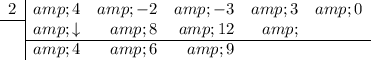
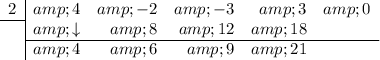
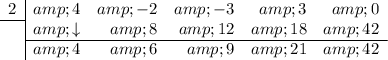
The last value, 42, is the value of the function when x is 2.

Therefore,

`f(2)=4x^4-2x^3-3x^2+3x=42`