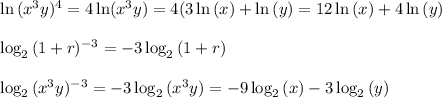Question

Give 3 examples each.​

Answer 1

see below

Explanation:

You want examples of use of the rules of logarithms:

`\begin{array}{ll}\vphantom{(M)/(gN)}1.&\log_b{(MN)}=\log_b{(M)}+\log_b{(N)}\\2.&\log_b{\left((M)/(N)\right)}=\log_b{(M)}-\log_b{(N)}\\\vphantom{(b)/(g)}3.&\log_b{(M^a)}=a\cdot\log_b{(M)}\end{array}`

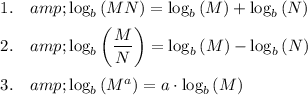
The point of these is that M and N and 'a' and 'b' can be anything. (Generally, 'b' will be a positive number greater than 1.) For the purpose here, we can let M ∈ {x^3y, (1+r)}, N ∈ {(x-4), r/n}, a ∈ {4, -3}, b ∈ {2, e}.

Using these values in various combinations, your examples could be ...

1. Product rule

`\log_2{((x^3y)(x-4))}=\log_2{(x^3y)}+\log_2{(x-4)}\\\\ln(((1+r)(r/n)))=ln((1+r))+ln((r/n))\\\\ \log_2{((x^3y)(r/n))}=\log_2{(x^3y)}+\log_2{(r/n)}`

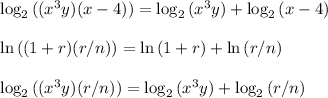
2. Quotient rule

`\log_2{\left((x^3y)/(x-4)\right)}=\log_2{(x^3y)}-\log_2{(x-4)}\\\\\\\ln{\left((1+r)/(r/n)\right)}=ln((1+r))-(ln((r))-ln((n)))\\\\\\ \log_2{\left((x^3y)/(r/n)\right)}=\log_2{(x^3y)}-(\log_2{(r)}-\log_2{(n)})}`

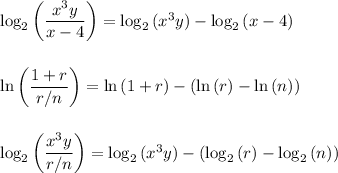
3. Power rule

`ln((x^3y)^4)=4\ln(x^3y)=4(3ln((x))+ln((y))=12ln((x))+4ln((y))\\\\\log_2{(1+r)^(-3)}=-3\log_2{(1+r)}\\\\\log_2{(x^3y)^(-3)}=-3\log_2{(x^3y)}=-9\log_2{(x)}-3\log_2{(y)}`