Answer:
a) $153,850
b) $779.54
c) $873.54
Explanation:
Part a)

Therefore, the loan amount is $153,850.
Part b)

Given:
- P = $153,850
- i = 0.045 per year = 0.045/12 per month
- n = 30 years = 360 months
Substitute the given values into the Monthly Payment formula and solve for PMT:
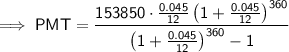
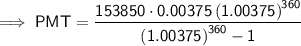
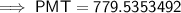
Therefore, the monthly payments would be $779.54.
Part c)
Given:
- P = $153,850
- i = 0.055 per year = 0.055/12 per month
- n = 30 years = 360 months
Substitute the given values into the Monthly Payment formula and solve for PMT:
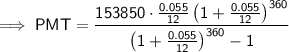
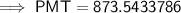
Therefore, the monthly payments would be $873.54.