Answer:
see explanation
Explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
(a)
given the equation of L1 is
2x - y = 3 ( subtract 2x from both sides )
- y = - 2x + 3 ( multiply through by - 1 )
y = 2x - 3 ← in slope- intercept form
with slope m = 2
• Parallel lines have equal slopes
then slope of L2 is m = 2
given the equation of L2 is
kx + 2y = 3 ( subtract kx from both sides )
2y = - kx + 3 ( divide through by 2 )
y = -
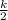 +
+
 ← in slope- intercept form
← in slope- intercept form
with slope m = -
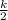
since slope of L1 and L2 are equal, both 2 , then
-
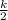 = 2 ( multiply both sides by 2 to clear the fraction )
= 2 ( multiply both sides by 2 to clear the fraction )
- k = 4 ( multiply both sides by - 1 )
k = - 4
----------------------------------------------
(b)
given the slope of a line is m then the slope of a line perpendicular to it is
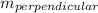 = -
= -
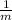 = -
= -

Then
for L2 to be perpendicular to L1
-
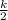 = -
= -
 ( multiply both sides by - 1 )
( multiply both sides by - 1 )
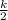 =
=
 , thus
, thus
k = 1