Let's consider an exponential decay function.
As an example, let's look at
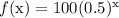
Here is a table of selected values:

As x gets bigger, y = f(x) is slowly approaching y = 0. It will never get to this exact value because we keep taking half of the previous y value (eg: we go from y = 25 to y = 12.5); there's no way to arrive at zero through this continuous halving process. If x/2 = 0, then x itself must be 0. But we started off with a nonzero value.
Visually, the curve is slowly approaching the x-axis. We say that the horizontal asymptote is y = 0 which is directly overlapping the x-axis. Think of the asymptote as an electric fence you can get closer to but not actually touch.
See the graph below. I used Desmos to create the graph.