Question

A worker will waterproof 4 commercial roofs if he spends 1 1/4 of waterproofing for each roof.

How many liters does he need to do the job?

If you already had 2 1/4 liters, then how much waterproofing do you need?

is fractions with procedure​

Answer 1

Problem with fractions:

-First question:

To calculate the number of liters, the number of roofs must be multiplied by the amount of waterproofing used for each roof.

To multiply the fractions, transform the mixed fractions to improper:

`\begin{gathered} \sf1 (1)/(4) * 4 = \\ \\ \sf (4 * 1 + 1)/(4) * (4)/(1) = \\ \\ \sf (4 + 1)/(4) * (4)/(1) = \\ \\ \sf(5)/(4) * (4)/(1) = \\ \\ \sf \frac {5 * 4}{4 * 1} = \\ \\ \boxed{ \sf \frac{ \red{20}}{ \red4}} = \sf \blue5\end{gathered}`

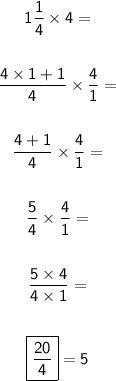
So you need five liters of waterproofing to get the job done.

-Second question:

To calculate the number of liters; It must be subtracted from the number of liters you need in total, which you already had or had:

`\begin{gathered} \sf5 - 2 (1)/(4) = \\ \\ \sf (5)/(1) - (4 * 2 + 1)/(4) = \\ \\ \sf\frac {5}{1} - (8 + 1)/(4) = \\ \\ \sf (5)/(1) - (9)/(4) = \\ \\ \sf(4 / 1 * 5 - 4 / 4 * 9)/(4) = \\ \\ \sf (20 - 9)/(4) = \\ \\ \boxed{ \sf (11)/(4)} = \boxed{ \sf \blue2 \: \: \blue{\sf(3 )/(4) }}\end{gathered}`

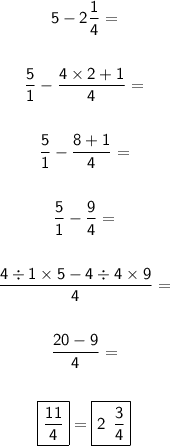
So, you need two whole and three quarter liters of waterproofing.