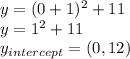Question

Find the standard form of an equation where a=1, and the vertex is at (-1,11). Find the x and y intercepts and graph the equation.

Answer 1

y =
`x^2+2x+12` (x and y intercepts under "Step-by-step explanation" section)

Explanation:

We can start by finding the vertex form and then expand it to the standard form.

The vertex form of the quadratic equation is

`y=a(x-h)^2+k`, where a is a constant and (h, k) is the vertex.

By plugging in 1 for a, -1 for h, and 11 for k, we have:

`y=1(x-(-1))^2+11\\y=(x+1)^2+11`

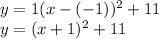
Now we simply expand this vertex form to get the standard form:

`y = (x+1)^2+11\\y=(x+1)(x+1)+11\\y=x^2+x+x+1+11\\y=x^2+2x+12`

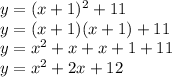
We can find the x and y-intercepts using the vertex form.

To find the x-intercept, we plug in 0 for y:

`0=(x+1)^2+11\\-11=(x+1)^2\\√(-11)=x+1;-√(11)=x+1\\ x_(intercepts):(-1+√(-11), 0); (-1-√(-11))`

The x-intercepts are non-real answers, so the quadratic equation never intersects the x-axis.

To find the y-intercept, we plug in 0 for x:

`y=(0+1)^2+11\\y=1^2+11\\y_(intercept) =(0,12)`