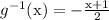Question

Are the following two functions inverse of one another ? If so tell why.

Answer 1

Answer: No, they are not inverses of one another.

=======================================================

Step-by-step explanation:

There are at least 3 methods we can use to prove the functions aren't inverses of each other.

------------------------------------

Method 1

Let's say we plugged x = 0 into f(x).

`f(\text{x}) = 2\text{x}+1\\\\f(0) = 2*0+1\\\\f(0) = 1\\\\`

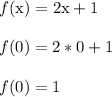
The input x = 0 leads to the output y = 1.

Then let's treat y = 1 as the input of the g(x) function, so we'll plug x = 1 into here.

`g(\text{x}) = -2\text{x}-1\\\\g(1) = -2*1-1\\\\g(1) = -3\\\\`

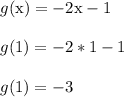
If g(x) was the inverse of f(x), then the g(1) output value should be 0 to get us back where we started. However, we get an output of -3 instead.

This is sufficient evidence to conclude that f(x) and g(x) are not inverses of each other. We only need one counter-example to disprove this claim.

------------------------------------

Method 2

Recall that if f(x) and g(x) are inverses of each other, then we have the following two properties

• f(g(x)) = x
• g(f(x)) = x

The left hand side of each equation involves the concept of "function composition".

Let's see what f(g(x)) is equal to in this case.

`f(\text{x}) = 2\text{x}+1\\\\f(g(\text{x})) = 2(g(\text{x}))+1\\\\f(g(\text{x})) = 2(-2\text{x}-1)+1\\\\f(g(\text{x})) = -4\text{x}-2+1\\\\f(g(\text{x})) = -4\text{x}-1\\\\`

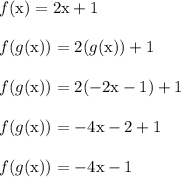
We do not get an output of simply x only, so this is another way to see how we don't have inverses.

Through similar steps, you should find that
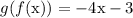`g(f(\text{x})) = -4\text{x}-3` which is further confirmation that f(x) and g(x) are not inverses of each other.

------------------------------------

Method 3

Let's ignore g(x) for now. We'll start with f(x) and find the inverse of it.

The process involves this basic outline:

1. Replace f(x) with y
2. Swap x and y
3. Solve for y

So,

`f(\text{x}) = 2\text{x}+1\\\\\text{y} = 2\text{x}+1\\\\\text{x} = 2\text{y}+1\\\\\text{x}-1 = 2\text{y}\\\\\text{y} = \frac{\text{x}-1}{2}\\\\f^(-1)(x) = \frac{\text{x}-1}{2}\\\\`

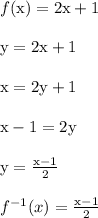
Unfortunately we do not end up with -2x-1 as the actual inverse.

So if
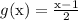`g(\text{x}) = \frac{\text{x}-1}{2}` was the case, then f(x) and g(x) would be inverses of each other.

Through similar steps, the inverse of
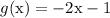`g(\text{x}) = -2\text{x}-1\\\\` is
`g^(-1)(\text{x}) = -\frac{\text{x}+1}{2}\\\\`