Answer:
6 drinks
2 boxes of candy
==================================================
Step-by-step explanation:
x = number of drinks
y = number of boxes of candy
These two variables represent positive integers.
"He bought 3 times as many drinks as candies" which means we can set up the equation x = 3y
-------------
1 drink costs $4.50
x drinks cost 4.50x dollars
1 box of candy costs $3
y boxes of candy cost 3y dollars.
4.50x + 3y = total cost = 33 dollars
Therefore, we arrive at the second equation of 4.50x+3y = 33
-------------
We have this system of equations

I'll use substitution to solve. Replace x with 3y in the second equation, then isolate y.
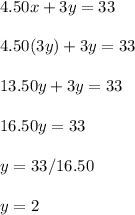
This tells us he bought 2 boxes of candy.
Use that value to find x.
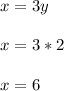
Carter also bought 6 drinks.
-------------------------------
Check:
- 6 drinks = 6*4.50 = 27 dollars
- 2 boxes of candy = 2*3 = 6 dollars
- Total cost = 27+6 = 33 dollars
The answers are confirmed.
Another way to confirm the answers is to plug (x,y) = (6,2) into each equation of the system I mentioned earlier. After simplifying, you should get the same thing on both sides.
A visual way to confirm the answers is to graph each equation on the same xy grid. The two lines intersect at (6,2). You can use a graphing tool such as Desmos or GeoGebra.