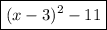Answer:
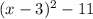
Explanation:
Given quadratic expression:
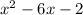
To write the given expression in the form (x + a)² + b, complete the square.
Add and subtract the square of half the coefficient of the term in x:
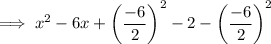
Simplify:
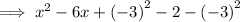
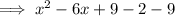
The first three terms x² - 6x + 9 form a perfect square trinomial.
A perfect square trinomial can be written as the square of a binomial.
Factor the perfect square trinomial:
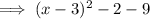
Simplify:
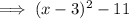
Therefore, the given expression written in the form (x + a)² + b is: