Answer:
Maria can buy at most 2 bottles of cranberry juice and 7 lemon-lime soda bottles.
Explanation:
Setting up the Solution
For this problem, we can set up an algebraic expression to represent the price, and this will help us solve the problem.
So firstly, let's assign the number of cranberry juice bottles to the variable "C". We could technically represent this as the variable name "cranberry juice bottles", but "C" is a bit more easier to write when writing an algebraic expression while still making it easy to distinguish. Let's also assign the number of lemon-lime soda to the variable "L".
Now let's find a way to express the price of each. The price of buying a certain amount of items, can generally be expressed as:
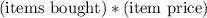 , since you have to pay the item price for each item bought, also known as, multiplication.
, since you have to pay the item price for each item bought, also known as, multiplication.
Since we know that the price of a cranberry juice bottle is $3.80 then that means the total amount used towards cranberry juice can be expressed as:
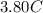 . We're just multiplying the number of cranberry juice bottles times the price. Likewise, we can represent the total amount used towards lemon-lime soda as:
. We're just multiplying the number of cranberry juice bottles times the price. Likewise, we can represent the total amount used towards lemon-lime soda as:
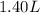 . The same logic is being applied here.
. The same logic is being applied here.
Now if we add both of these, we get the total amount that will be spent which is:
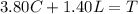 , and in this case I just set it equal to "T" which just represents the total spent.
, and in this case I just set it equal to "T" which just represents the total spent.
Now there's two more things to do. Generally we can't really solve two-variable equations and we want to express one variable in terms of the other, so that we can rewrite the equation as a one-variable equation.
There is one piece of information given that allows us to do this. "The recipe calls for 3.5 times as many bottles of lemon-lime soda as cranberry". So we can represent the numbers of lemon-lime soda bottles as 3.5 times the amount of cranberry juice bottles. We can express it as:

So now let's plug this into the equation, instead of "L". This gives us:
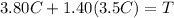
let's multiply the 1.40 by the 3
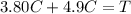
now let's add up the values.
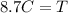
Now lastly, this represents the total amount that is going to be spent. Since Maria only has $17.40, we want this total to be less than or equal to 17.40 (assuming there is no sales tax, but this was never given). this gives us our final expression we will be using:
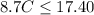
Solving the Problem
From here solving the problem is actually pretty easy. Think of the inequality as a linear equation, we can still apply the same (for the most part) algebraic manipulations we apply to linear equations. We just divide both sides by 8.7 to isolate the C
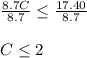
So Maria can buy a maximum of 2 bottles of cranberry juice. From this we can actually determine the number of lemon-lime soda bottles.
So we know that:
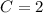
From this we can determine what L is, since remember the equation we set up earlier?
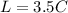
Let's just plug C into the equation, and we get:
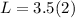
Multiply
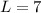
So Maria can buy at most 2 bottles of cranberry juice and 7 lemon-lime soda bottles.