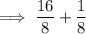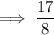Question

NO LINKS! PLEASE HELP ME!​

Answer 1

`(17)/(8)`

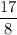
Explanation:

Given statement:

• The quotient of (8/5 divided by 8/10) is added to the product of (8/14 × 7/12 × 3/8):

`\implies ((8)/(5))/((8)/(10))+\left((8)/(14) * (7)/(12) * (3)/(8)\right)`

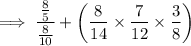
To divide two fractions, flip the second fraction (make the numerator the denominator, and the denominator the numerator) then multiply it by the first fraction:

`\implies \left((8)/(5) * (10)/(8)\right)+\left((8)/(14) * (7)/(12) * (3)/(8)\right)`

`\textsf{Apply the fraction rule} \quad (a)/(c)*(b)/(d)=(ab)/(cd):`

`\implies \left((8 * 10)/(5* 8)\right)+\left((8 * 7 * 3)/(14 * 12 * 8)\right)`

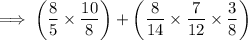
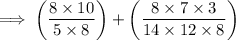
Carry out the multiplications:

`\implies (80)/(40)+(168)/(1344)`

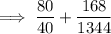
Simplify the fractions by dividing the numerator and denominator by the GCF:

`\implies (80 / 40)/(40/ 40)+(168 / 168)/(1344 / 168)`

`\implies (2)/(1)+(1)/(8)`

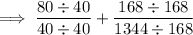
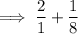
Make the denominators of both fractions the same:

`\implies (2 * 8)/(1* 8)+(1)/(8)`

`\implies (16)/(8)+(1)/(8)`

`\textsf{Apply the fraction rule} \quad (a)/(c)+(b)/(c)=(a+b)/(c):`

`\implies (16+1)/(8)`

`\implies (17)/(8)`